Física y matemáticas
Según Galileo Galilei: “Las Matemáticas son el lenguaje con el que el Dios ha escrito el universo”. Aunque esta afirmación es dudosa, por la supuesta intervención de un “escritor” de la naturaleza y un lenguaje en que escribe, las matemáticas son, sin duda, el lenguaje en que nosotros expresamos nuestro conocimiento de la naturaleza (en griego naturaleza es φυσικός [fysikós]). Así, en Ciencia, a la que llamaré genéricamente “Física”, las leyes de la naturaleza, se expresan de manera condensada en lenguaje matemático, lo que permite desarrollarlas y obtener consecuencias de las mismas, mediante el razonamiento lógico-matemático que es riguroso y “exacto”[1]. De aquí que las matemáticas se denominen a menudo “ciencias exactas”. La exactitud de las matemáticas se deriva, a mi entender, de que no tratan con objetos naturales, sino con creaciones de la mente humana, que se establecen de manera exacta con sus propiedades y características “a priori”, sin necesidad de que tengan correlación alguna con la naturaleza. Así, por poner un ejemplo sencillo, los números complejos o imaginarios, son realmente unos objetos imaginados por nosotros, que muestran propiedades bastante complejas, poco imaginadas en principio, pero que se deducen lógicamente de su definición. Otra cosa es que, en algunos casos, las propiedades de estos números, represente las propiedades, por ejemplo, de las ondas, y sirvan para describirlas y deducir su comportamiento.
Las matemáticas representan la naturaleza, siempre que los fenómenos naturales se ajusten a las definiciones y leyes de los objetos matemáticos con exactitud. En muchos casos, la física (ciencia natural) se ha visto obligada a desarrollar nuevas matemáticas para poder expresar y razonar sobre sus descubrimientos, pues no encontraba objetos y herramientas matemáticas disponibles que se ajustaran a los fenómenos y leyes que descubría.
Las herramientas matemáticas han tenido, en gran medida, un desarrollo paralelo al de la Física. Los griegos razonaban matemáticamente (calculaban) mediante construcciones geométricas [2]. Un ejemplo pionero es el cálculo del radio de la tierra por Eratóstenes, en el s III a.C. El uso de la aritmética, donde los números estaban representados por letras del alfabeto (probablemente tomados de los egipcios), como sucede con los romanos, era muy rudimentario y los cálculos más simples (sumas y restas) se realizaban con ábacos, pues el procedimiento escrito era muy complicado [3]. Las multiplicaciones eran aún más complicadas y las divisiones solamente se podían hacer por tanteos sucesivos. Esta dificultad se solventó con los dígitos decimales o guarismos, que se desarrollaron en la India alrededor del siglo V a.C. Los árabes, modificaron la forma de las cifras (llamadas ghobar) y lo introdujeron en Europa mucho más tarde (siglo X), a través de España
El cálculo deferencial (derivadas) fue desarrollado por Newton hacia 1665, para explicar sus teorías sobre el movimiento y la gravedad, pero fue Leibniz quien lo publicó primero, lo que generó una controversia sobre quién lo inventó. En todo caso es un ejemplo de desarrollo matemático alcanzado por necesidad de expresar leyes naturales
Otros casos, menos comunes, son los de leyes empíricas expresadas con lenguaje común, sin matemáticas, en general por ignorar las matemáticas necesarias. Faraday, por ejemplo, era un científico experimental sin ninguna formación en matemáticas, pues era encuadernador antes de entrar en la Royal Institution como ayudante de Humphry Davy, al que sucedió en el puesto de director de la misma. A pesar de su ignorancia de las matemáticas, consiguió encontrar muchos fenómenos nuevos en electricidad y magnetismo y algunas de las leyes más famosas en su campo como las de la electrólisis, el paramagnetismo y diamagnetismo y la inducción electromagnética.
Faraday observó e investigó por primera vez el fenómeno de la inducción electromagnética, hacia 1830 [4] mediante experimentos con imanes y bobinas (figura).
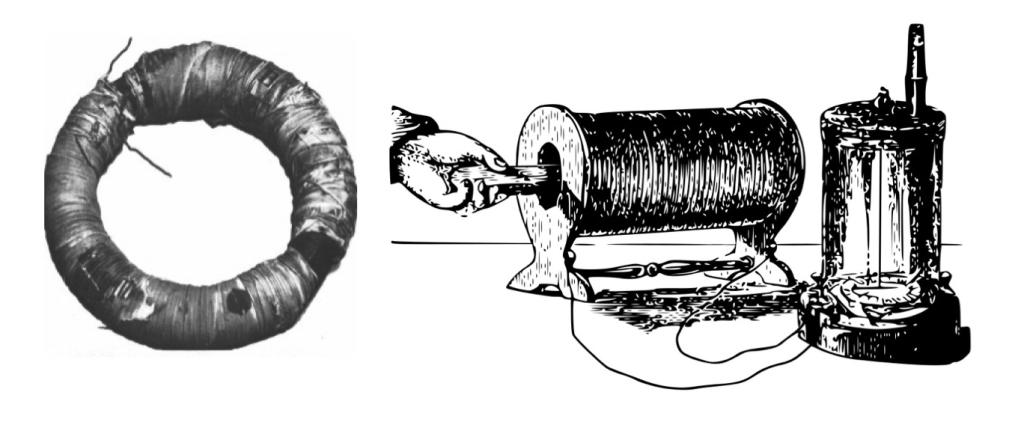
Izquierda: Anillo de hierro original de Faraday con las dos bobinas de cobre arrolladas sobre él, tal como se conserva en la Royal Institution. Derecha: Experimento de la barra de imán y la bobina
Su formulación de la ley está hecha en función de las llamadas líneas de fuerza o inducción magnética, unas líneas imaginarias que seguían la dirección en la que apuntaría una pequeña brújula. Tuvo que inventar el concepto visual y espacial de las líneas de fuerza para poder describir y trabajar con fenómenos eléctricos y magnéticos sin usar matemáticas. Para describir sus hallazgos, Faraday utilizaba expresiones como la siguiente:
«Siempre que el número de líneas de fuerza magnética que pasan a través de un circuito conductor cambia (aumenta o disminuye), se establece una fuerza electromotriz (fem) o tensión en el circuito.»
Tuvo que ser el físico escocés James Clerk Maxwell quien formuló la expresión matemática que relaciona la variación del flujo magnético (Φ) que es una forma matemática de expresar el número de líneas magnéticas que atraviesan un circuito, con la fuerza electromotriz inducida (fem), de la forma:
fem = −dΦ/dt .
Aquí dΦ/dt representa la derivada, la forma matemática de expresar la tasa de variación, del flujo respecto al tiempo. La ley de Faraday es una de las cuatro ecuaciones de Maxwell que definen la teoría electromagnética e incluyen también la ley de Gauss y la de Ampere, que completó Maxwell. Tanto Gauss como Ampere habían formulado sus leyes matemáticamente, pues no carecían precisamente de formación en este tema. Las ecuaciones de Maxwell le permitieron descubrir que la luz era una onda electromagnética, lo que hubiera sido imposible a partir de la ley de Faraday expresada sin matemáticas.
Cuando Einstein, que tampoco era buen matemático, formuló su teoría de la relatividad, usó una notación sencilla, parecida a la de Maxwell, pero posteriormente introdujo la notación tensorial, en 4 dimensiones: tres espaciales más el tiempo. Con dicha notación, las 4 ecuaciones de Maxwell se reducen solamente a dos:
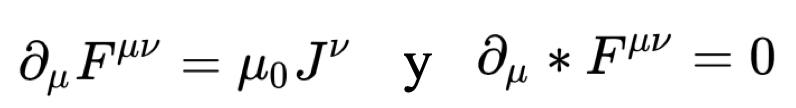
Donde F es el tensor campo electromagnético, de 16 componentes, y J incluye las cargas y corrientes en un vector de 4 componentes. La ley de Faraday está incluida en la segunda ecuación. Esta notación muestra directamente la invariancia las ecuaciones de Maxwell en cualquier sistema de referencia inercial, que es precisamente lo que postula la teoría de la relatividad.
Es evidente que las matemáticas son una gran ayuda para expresar y deducir conclusiones a partir de las leyes de la naturaleza, siempre que la naturaleza se ajuste a las relaciones entre los correspondientes objetos matemáticos. La Física tiene en cuenta esta correspondencia entre objetos reales y matemáticos y también otras propiedades de los objetos físicos, que se expresan en otras leyes. Los matemáticos solamente se ocupan de las relaciones exactas entre objetos matemáticos, que algunas veces no agotan la complejidad del mundo real, o que, muy raramente, la superan.
Para traducir la naturaleza a matemáticas necesitamos una tabla con el código de correspondencia entre ambas. Luego, al revertir las consecuencias matemáticas al mundo real (físico), hay que saber adecuar los resultados a la realidad. En algunas ocasiones hay un grupo de soluciones matemáticas que no tiene sentido físico, por lo que se descartan sin más. Hay, al menos, un caso interesante en que las soluciones absurdas (al parecer) revelaron fenómenos desconocidos hasta el momento. Me refiero a la predicción de la Mecánica Cuántica Relativista de Dirac, de que hay una infinidad de soluciones de las ecuaciones para electrones con energías negativas. Dirac podría haber desechado estas soluciones por irreales, pero postuló que los electrones con energías negativas serían “invisibles” por estar “ocupando” todos sus posibles estados, de manera que había un “mar” de infinitos electrones que serviría de fondo a la realidad observable. Dirac propuso asimismo la existencia de una nueva partícula muy similar al electrón, pero de carga positiva (el positrón), que aparecería cuando se hiciera un hueco en ese “mar” de electrones negativos por aumentar la energía de alguno de ellos hasta hacerse positiva. Esta interpretación, confirmada más tarde al descubrirse el experimentalmente la existencia del positrón, predijo la existencia de la “antimateria”, hoy en día perfectamente integrada entre los fenómenos naturales, en una expresión matemática menos chocante que la del mar infinito de electrones con energía negativa.
Hegel tenía una visión francamente optimista de la capacidad de entender el mundo de manera lógica, expresada por su sentencia: “todo lo real es racional”. Sin embargo, Hegel incluía además la opuesta “todo lo racional es real”. Yo entendería que quería decir que cualquier resultado matemático o incluso filosófico, no contradictorio, existe en algún sitio, pero probablemente no quería decir eso. No me siento capaz de leer a Hegel a ver qué quería decir (recuerdo que era muy difícil de entender, cuando lo estudiaba en bachillerato), así que he preguntado a ChatGPT, que me dice:
Hegel no quería decir que cualquier resultado matemático posible, o cualquier idea no contradictoria, existe literalmente en algún lugar del universo. Su frase “todo lo racional es real, y todo lo real es racional” suele malinterpretarse si se lee con el sentido moderno de “racional = lógico o matemáticamente consistente” y “real = existe físicamente”.
Y luego trata de explicarme que: Lo racional es la estructura profunda del desarrollo del Espíritu, el proceso mediante el cual la realidad (histórica, social, política, conceptual) llega a expresarse de forma autoconsciente.
Mientras que lo real es: aquello que ha adquirido efectividad (Wirklichkeit), es decir, que se ha integrado en la vida histórica, social, institucional, conceptual del Espíritu. Algo puede “existir físicamente” y aun así no ser real en el sentido hegeliano, si no expresa una forma necesaria del Espíritu.
Bueno, pues ya me parecía que iba a ser algo más complicado, aunque tras la explicación, sigo sin entenderlo, como me temía. Sin embargo, hay una parte de los científicos, los llamados “físicos teóricos” (aunque afortunadamente no todos ellos ni mucho menos), que parecen creer en la interpretación “dura” de Hegel, en el sentido de que sus teorías matemáticas tienen que ser reales (en sentido que verdaderas) aunque no encuentren los objetos que aparecen en ellas. Por ejemplo, quieren creer que es mejor, más simétrico y compacto que las cuatro fuerzas de la naturaleza se unifiquen dando lugar a un esquema más sencillo y elegante. Existe una tendencia a considerar más plausibles las teorías que presentan simplicidad, elegancia y simetría, incluso antes de que haya evidencia empírica, y que la belleza matemática es una guía hacia teorías verdaderas. Así ha sucedido con
Las Supercuerdas, una teoría simétrica, unificadora, que postula partículas como las correspondientes a una infinidad de modos vibracionales de estas cuerdas de 11 dimensiones, que no han sido observadas. A pesar de ello, era “tan consistente y elegante que debería de ser correcta”.
La Supersimetría entre fermiones y bosones, que Implicaba nuevas partículas, las compañeras supersimétricas de las actuales, como sleptones, gluinos, higgsinos, winos, binos, gravitinos, nunca encontradas, pero que se justificaba por su “naturalidad” y elegancia.
Las Teorías de Gran Unificación de las fuerzas, que hemos comentado antes, que predicen simetrías y partículas que tampoco aparecen, aunque estas teorías tienen como atractivo la simplicidad de unir todas las fuerzas en una única.
En cosmología hay varias Teorías del Multiverso, que viene a decir que existen muchos (potencialmente infinitos) universos paralelos , pero inalcanzables. Estas teorías no solamente no han sido comprobadas, sino que incluyen un aspecto peor: nunca podrán ser comprobables pues no tenemos acceso a los otros universos por lo que quedan fuera de la realidad.
Bien, no es cuestión de alargarse con estas múltiples teorías “racionales” que no parecen en absoluto “reales”. Mejor recuperar un excelente físico teórico (Richard Feynman) que no se dejó arrastrar por la belleza y elegancia de estas y otras teorías, pues, en su concepción de la ciencia: “No importa lo hermosa que sea tu teoría, no importa lo inteligente que seas. Si no está de acuerdo con el experimento, está mal”
NOTAS
[1] No es este lugar para explayarnos en los problemas internos de la lógica matemática, expresados en los teoremas de incompletitud de Gödel, descubiertos por este matemático- lógico y filósofo en 1931, al tratar de dar una base universal al razonamiento lógico-matemático. Quizá en algún momento lo ataque, pero el asunto es bastante peliagudo y me llevará aún mucho tiempo el entenderlo, si finalmente lo consigo.
[2] https://www.reddit.com/r/math/comments/xcggtq/how_did_ancient_greek_do_calculations/?tl=es-es
[3] https://www.gaussianos.com/operar-con-numeros-romanos/
[4] M. Faraday, Experimental Researches in Electricity, vol. III, Taylor and Francis, London 1855
